1. Introduction.

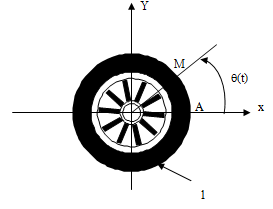
Soit un solide 1 en rotation autour d’un axe z passant par O, la trajectoire des points M du solide est un cercle de centre O et de rayon OM. A t = 0 s, M est en A (position initiale). A t quelconque, M a décrit un arc de cercle.

Abscisse curviligne de M (se dit de la longueur d’un arc de cercle).

                       s(M) = R. θ  Unités : S(M) en m, R en m, θ  en rad

1. Vitesse de rotation ou vitesse angulaire ω.

La vitesse de rotation ω1/0 (ou θ’1/0) du solide 1 en rotation par rapport au solide de référence 0 est égale à la dérivée par rapport au temps de l’angle de rotation θ1/0 = f (t) .

                                                                   

ω1/0 = θ’1/0                Unité légale le radian par seconde noté rad/s.

       La vitesse de rotation décrit ou traduit les variations de l’angle de rotation θ1/0.

1. Accélération angulaire θ’’1/0.

L’accélération angulaire θ’‘1/0 d’un solide 1 en rotation par rapport à un solide  de référence 0 est égale à la dérivée par rapport au temps de la vitesse de rotation ω1/0.

                                                                     

θ"1/0  =  ω’1/0        Unité légale le radian par seconde carré rad/s²

Remarque : θ"1/0 est aussi égale à la dérivée seconde de l’angle de rotation θ1/0.

L’accélération angulaire décrit ou traduit les variations de la vitesse de rotation ω1/0.

1. Vecteur accélération

On montre que le vecteur accélération en un point d’un solide en rotation se décompose en deux parties distinctes.

1. Accélération normale

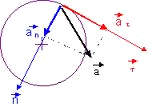
                       Point d’application : M

                       Direction : sur le rayon

AnM1/0

                       Sens : vers le centre du cercle

                       Module : ω².R = V²/R

1. Accélération tangentielle

                       Point d’application : M

                       Direction : sur la tangente

AtM1/0        Sens :        celui du mouvement en accélération

                               inverse au mouvement en décélération

                       Module :  ω’.R

A = At + An = ω².R.n + ω’.R.t

Créé avec HelpNDoc Personal Edition: Produire facilement des livres électroniques Kindle